3496. Подмножество сумм

Набор последовательных целых чисел от 1 до n можно разбить на два подмножества так, чтобы суммы их элементов совпадали.

Например для n = 3 можно совершить следующее разбиение множества {1, 2, 3} на подмножества с равными суммами:

· {3} и {1, 2}

Это считается одним разбиением (т. е. аналогичное разбиение в обратном порядке считается как одно разбиение и, следовательно, не увеличит количество разбиений).

При n = 7 существует четыре способа разбиения множества {1, 2, 3, ..., 7} на подмножества с равными суммами:

· {1, 6, 7} и {2, 3, 4, 5}

· {2, 5, 7} и {1, 3, 4, 6}

· {3, 4, 7} и {1, 2, 5, 6}

· {1, 2, 4, 7} и {3, 5, 6}

Для заданного n необходимо вывести количество способов разбиения множества, содержащего все целые числа от 1 до n, на две группы так, что суммы элементов этих подмножеств совпадали. Вывести 0, если таких способов не существует.

Вход. Целое число n (1 ≤ n ≤ 39).

Выход. Количество способов, которыми можно совершить разбиение исходного множества {1, 2, ..., n} на два подмножества так, что суммы элементов этих подмножеств будут одинаковы. Вывести 0, если требуемого разбиения не существует.

Пример входа	Пример выхода
7	4

РЕШЕНИЕ

динамическое програмиирование

Анализ алгоритма

Пусть s – сумма всех целых чисел от 1 до n. Если s нечетно, то ответ 0. Иначе ответ равен количеству способов, которыми можно выбрать подмножество с суммой элементов s / 2, деленному на 2. Последнее следует совершить чтобы разбиения A È B и B È A считать одинаковыми.

Пусть m[s] содержит количество способов, которыми можно набрать подмножество с суммой s из множества {1, 2, ..., n}. Изначально положим m[0] = 1.

Пусть массив m уже заполнен требуемым образом для чисел из множества {1, 2, ..., i – 1}. Приходит следующее число i. Тогда ко всякому значению m[j] (i ≤ j < MAX) следует прибавить m[j – i].

Пример

Пусть n = 7. Сумма всех чисел от 1 до 7 равна (1 + 7) / 2 * 7 = 28. Вычислим количество способов составить подмножество с суммой элементов 14.

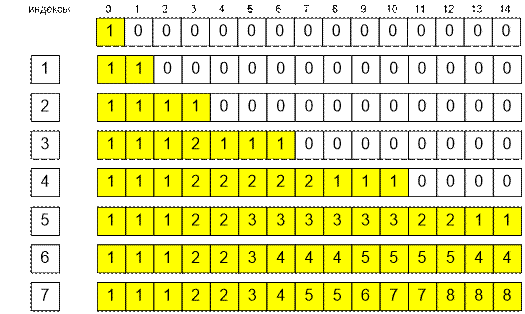
После обработки множества {1, 2} имеем следующее состояние массива:

· m[0] = 1: сумма 0 представляется пустым подмножеством;

· m[1] = 1: сумма 1 представляется подмножеством {1};

· m[2] = 1: сумма 2 представляется подмножеством {2};

· m[3] = 1: сумма 3 представляется подмножеством {1, 2};

Приходит следующий элемент множества i = 3. Ко всякому значению m[j] (3 ≤ j < MAX) следует прибавить m[j – 3]. Ненулевыми m[j] будут следующие:

· m[6] = m[6] + m[3] = 0 + 1 = 1, подмножество {1, 2, 3};

· m[5] = m[5] + m[2] = 0 + 1 = 1, подмножество {2, 3};

· m[4] = m[4] + m[1] = 0 + 1 = 1, подмножество {1, 3};

· m[3] = m[3] + m[0] = 1 + 1 = 2, подмножества {1, 2}, {3};

Реализация алгоритма

Объявим рабочий массив.

#define MAX 1001

long long m[MAX];

Читаем значение n.

scanf("%lld",&n);

Инициализируем и заполняем массив m.

memset(m,0,sizeof(m)); m[0] = 1;

for(i = 1; i <= n; i++)

for(j = MAX - 1; j >= i; j--) m[j] += m[j - i];

Вычисляем сумму чисел от 1 до n. Выводим результат.

s = (1 + n) * n / 2;

if (s % 2 == 1) printf("0\n");

else printf("%lld\n",m[s/2]/2);